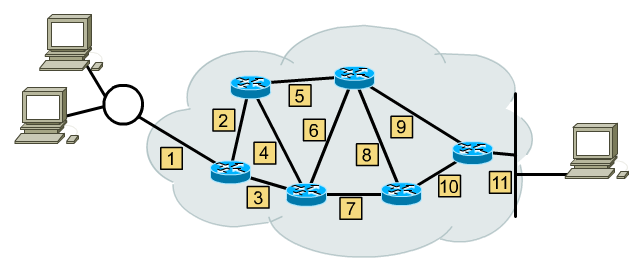
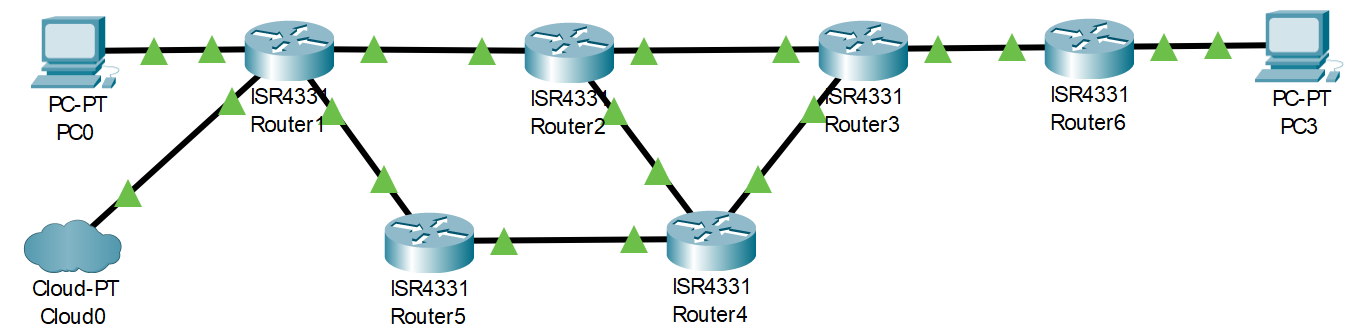
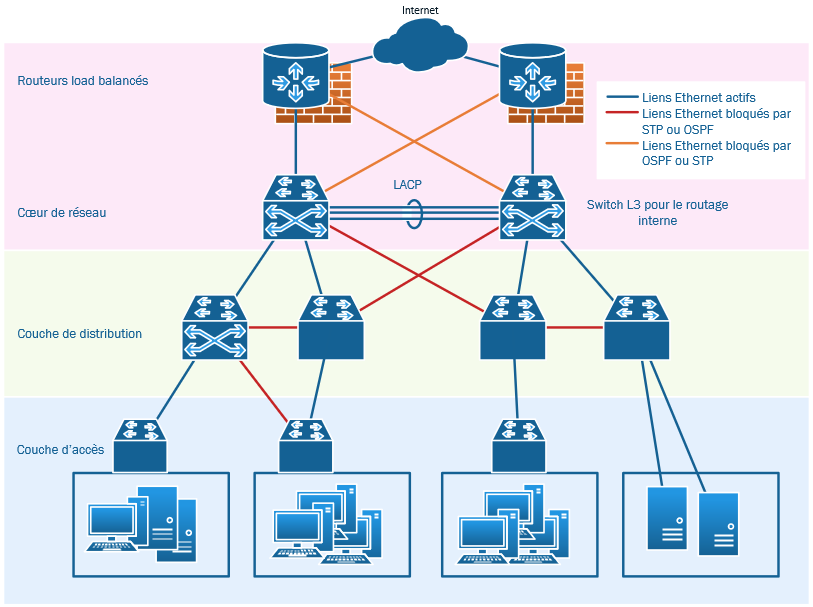
Voir aussi le diaporama de cours, vue ... en cours
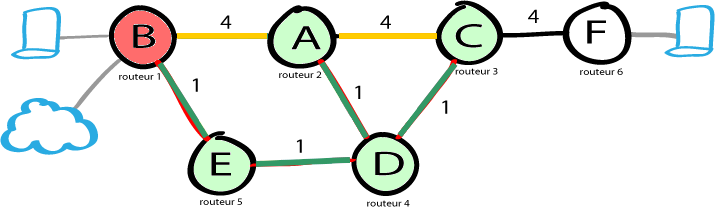
Le réseau (info) précédent nous donne le réseau (math) suivant :
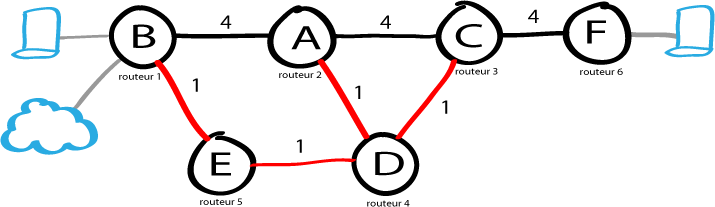
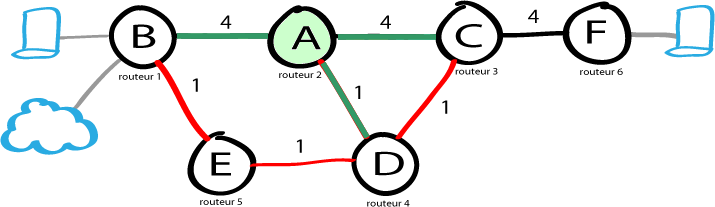
Le routeur 2 est arbitrairement choisi comme source. Les liens rouges sont des fibres optiques en 10Gbps, le reste sont des liens en 1Gbps
L'algorithme global est le suivant :
Valeurs des métriques des liens
| Bande passante | coût attribué |
|---|
| 10Gb | 1 |
| 1Gb | 4 |
- L'algo commence essentiellement au nœud choisi (source). Il analyse ensuite le graphe du réseau pour trouver le chemin le plus court entre ce nœud et tous les autres nœuds.
- L'algo garde la trace de la distance la plus courte actuellement connue entre chaque noeud et le noeud source et met les valeurs à jour s'il trouve un chemin plus court.
- Quand l'algorithme a trouvé le chemin le plus court entre le nœud source et un autre nœud, ce nœud est marqué comme "visité" et ajouté au chemin final.
- L'algo traite chaque nœud jusqu'à ce que tous les nœuds aient été ajoutés au chemin.
Nous obtenons alors un chemin qui relie le nœud source à tous les autres nœuds en suivant le chemin le plus court possible pour atteindre chaque nœud.
Appliquons les DA (calculées avec les métriques d'OSPF) au liens du routeur 2 :
Etape 1 : A
Phase 1 : déterminer la source
On a notre routeur Source : le routeur 2 (repéré A), choisi arbitrairement.
Pour chaque chemin vers un autre routeur, on aura un couple de données : (parent, poids) qui correspond au parent du routeur dans le chemin et au poids du lien pour le rejoindre.
Initialisation : au début, tous les couples ont un poids infini car on ne connait pas de chemin idéal. Le parent est aussi inconnu.

| Étape | Noeuds | A | B | C | D | E | F |
|---|
| Coût depuis A | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ |
|---|
| Chemin depuis A | {Ø} | {Ø} | {Ø} | {Ø} | {Ø} | {Ø} |
|---|
| Init | {A, B, C, D, E, F} | (Ø, ∞) | (Ø, ∞) | (Ø, ∞) | (Ø, ∞) | (Ø, ∞) | (Ø, ∞) |
| 1 : ? | | | | | | | |
Phase 2 : calcul des coûts
On peut noter tous les enfants ayant A pour parent. C'est-à-dire les noeuds B, C et D ou routeurs 1, 3 et 4.
Pour chaque chemin vers A, on valide le couple de données : (A, poids du lien) correspondant.
| Étape | Noeuds | A | B | C | D | E | F |
|---|
| Coût depuis A | 0 | 4 | 4 | 1 | ∞ | ∞ |
|---|
| Chemin depuis A | {A} | {A,B} | {A,C} | {A,D} | {Ø} | {Ø} |
|---|
| Init | {A, B, C, D, E, F} | (Ø, ∞) | (Ø, ∞) | (Ø, ∞) | (Ø, ∞) | (Ø, ∞) | (Ø, ∞) |
| 1 : A | {B, C, D, E, F} | (A, 0) | (A, 4) | (A, 4) | (A, 1) | (Ø, ∞) | (Ø, ∞) |
| 2 : ? | | | | | | | |
Etape 2 : D
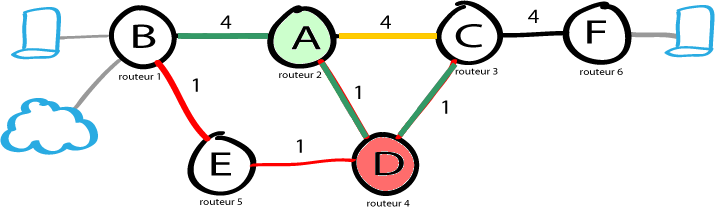
On va traiter le noeud D, c'est le moins cher (routeur 4).
Le poids du lien sera augmenté du coût nécessaire pour aller du noeud parent du noeud courant : le noeud A est le parent du noeud C.
Ainsi, le lien vers E aura un coût de 1 (le lien)+1 (le coût de A vers D).
Pour chaque chemin depuis D (vers C et E), on valide le couple de données : (D, poids du lien) correspondant. Sauf que ...
Sauf que C a déjà un couple formé. On prenda donc le couple dont le coût est le moins cher. C'est-à-dire : (D, 2)
| Étape | Noeuds | A | B | C | D | E | F |
|---|
| Coût depuis A | 0 | 4 | 2 | 1 | 2 | ∞ |
|---|
| Chemin depuis A | {A} | {A,B} | {A,D,C} | {A,D} | {A,D,E} | {Ø} |
|---|
| Init | {A, B, C, D, E, F} | (Ø, ∞) | (Ø, ∞) | (Ø, ∞) | (Ø, ∞) | (Ø, ∞) | (Ø, ∞) |
| 1 : A | {B, C, D, E, F} | (A, 0) | (A, 4) | (A, 4) | (A, 1) | (Ø, ∞) | (Ø, ∞) |
| 2 : D | {B, C, E, F} | (A, 0) | (A, 4) | (D, 2) | (A, 1) | (D, 2) | (Ø, ∞) |
| 3 : ? | | | | | | | |
On valide le noeud D.
Etape 3 : E ou C ?
Bon, maintenant, nous avons le choix entre traiter E ou C. Le choix se fera sur le coût le plus faible ou, à défaut, sur la lettre la plus petite (il faut bien faire un choix ...).
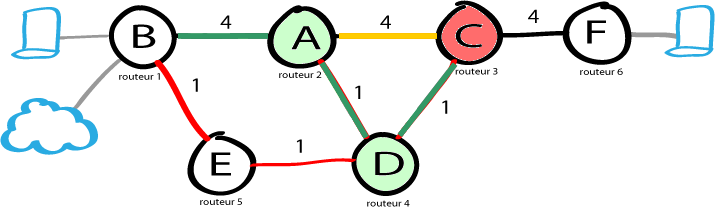
On va donc traiter le noeud C.
Pour chaque chemin depuis C (vers A et F), on valide le couple de données : (C, poids du lien) correspondant. Sauf que ...
- Vers A, le coût est de 8 et A est déja "visité" donc on ne change rien.
- Vers F, le coût est de 6 (2+4), donc on affecte la valeur comme elle est inférieure à "l'infini".
Sauf que A a déjà un couple formé et est "visité". On ne pourra pas toucher les valeurs de A et de toute façon, le coût existant est infrieur à celui que l'on vient de calculer
| Étape | Noeuds | A | B | C | D | E | F |
|---|
| Coût depuis A | 0 | 4 | 2 | 1 | 2 | 6 |
|---|
| Chemin depuis A | {A} | {A,B} | {A,D,C} | {A,D} | {A,D,E} | {A,D,C,F} |
|---|
| Init | {A, B, C, D, E, F} | (Ø, ∞) | (Ø, ∞) | (Ø, ∞) | (Ø, ∞) | (Ø, ∞) | (Ø, ∞) |
| 1 : A | {B, C, D, E, F} | (A, 0) | (A, 4) | (A, 4) | (A, 1) | (Ø, ∞) | (Ø, ∞) |
| 2 : D | {B, C, E, F} | (A, 0) | (A, 4) | (D, 2) | (A, 1) | (D, 2) | (Ø, ∞) |
| 3 : C | {B, E, F} | (A, 0) | (A, 4) | (D, 2) | (A, 1) | (D, 2) | (C, 6) |
| 4 : | | | | | | | |
On valide le noeud C.
Pour la suite, on ne suit pas le chemin vers F car tous les chemins de D ne sont pas explorés.
Etape 4 : E, le second bord
Bon, maintenant, C est validé, .
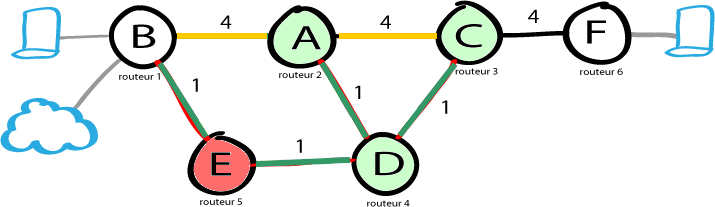
On va donc traiter le noeud E, qui est le second enfant de D.
Pour chaque chemin depuis C (vers A et F), on valide le couple de données : (C, poids du lien) correspondant. Sauf que ...
- Vers B, le coût est de 3, on met B à jour.
C'est tout ici.
| Étape | Noeuds | A | B | C | D | E | F |
|---|
| Coût depuis A | 0 | 3 | 2 | 1 | 2 | 6 |
|---|
| Chemin depuis A | {A} | {A,D,E,B} | {A,D,C} | {A,D} | {A,D,E} | {A,D,C,F} |
|---|
| Init | {A, B, C, D, E, F} | (Ø, ∞) | (Ø, ∞) | (Ø, ∞) |
(Ø, ∞) | (Ø, ∞) | (Ø, ∞) |
| 1 : A | {B, C, D, E, F} | (A, 0) | (A, 4) | (A, 4) | (A, 1) | (Ø, ∞) | (Ø, ∞) |
| 2 : D | {B, C, E, F} | (A, 0) | (A, 4) | (D, 2) | (A, 1) | (D, 2) | (Ø, ∞) |
| 3 : C | {B, E, F} | (A, 0) | (A, 4) | (D, 2) | (A, 1) | (D, 2) | (C, 6) |
| 4 : E | {B, F} | (A, 0) | (E, 3) | (D, 2) | (A, 1) | (D, 2) | (C, 6) |
| 5 : ? | | | | | | | |
On valide le noeud E.
Etape 5 : B, le plus petit coût
B est plus petit que F donc on passe par là
Mais pour B ...
- le chemin vers A : déjà vu.
- pas d'autre chemin, internet est hors de notre zone.
Il ne reste aucun noeud à visiter et on peut valider B.
| Étape | Noeuds | A | B | C | D | E | F |
|---|
| Coût depuis A | 0 | 3 | 2 | 1 | 2 | 6 |
|---|
| Chemin depuis A | {A} | {A,D,E,B} | {A,D,C} | {A,D} | {A,D,E} | {A,D,C,F} |
|---|
| Init | {A, B, C, D, E, F} | (Ø, ∞) | (Ø, ∞) | (Ø, ∞) |
(Ø, ∞) | (Ø, ∞) | (Ø, ∞) |
| 1 : A | {B, C, D, E, F} | (A, 0) | (A, 4) | (A, 4) | (A, 1) | (Ø, ∞) | (Ø, ∞) |
| 2 : D | {B, C, E, F} | (A, 0) | (A, 4) | (D, 2) | (A, 1) | (D, 2) | (Ø, ∞) |
| 3 : C | {B, E, F} | (A, 0) | (A, 4) | (D, 2) | (A, 1) | (D, 2) | (C, 6) |
| 4 : E | {B, E, F} | (A, 0) | (E, 3) | (D, 2) | (A, 1) | (D, 2) | (C, 6) |
| 5 : B | {B, F} | (A, 0) | (E, 3) | (D, 2) | (A, 1) | (D, 2) | (C, 6) |
| 6 : ? | | | | | | | |
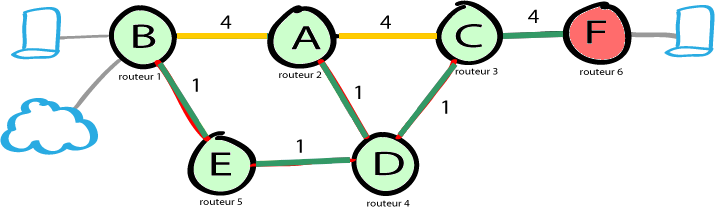
Etape 6 : F, dernière étape
F, comme B, est une routeur de bord de zone (ABR et même ASBR). Il n'y a auncun autr neod à visiter. On peut valider F.
| Étape | Noeuds | A | B | C | D | E | F |
|---|
| Coût depuis A | 0 | 3 | 2 | 1 | 2 | 6 |
|---|
| Chemin depuis A | {A} | {A,D,E,B} | {A,D,C} | {A,D} | {A,D,E} | {A,D,C,F} |
|---|
| Init | {A, B, C, D, E, F} | (Ø, ∞) | (Ø, ∞) | (Ø, ∞) | (Ø, ∞) | (Ø, ∞) | (Ø, ∞) |
| 1 : A | {B, C, D, E, F} | (A, 0) | (A, 4) | (A, 4) | (A, 1) | (Ø, ∞) | (Ø, ∞) |
| 2 : D | {B, C, E, F} | (A, 0) | (A, 4) | (D, 2) | (A, 1) | (D, 2) | (Ø, ∞) |
| 3 : C | {B, E, F} | (A, 0) | (A, 4) | (D, 2) | (A, 1) | (D, 2) | (C, 6) |
| 4 : E | {B, E, F} | (A, 0) | (E, 3) | (D, 2) | (A, 1) | (D, 2) | (C, 6) |
| 5 : B | {B, E, F} | (A, 0) | (E, 3) | (D, 2) | (A, 1) | (D, 2) | (C, 6) |
| 6 : F | {B, F} | (A, 0) | (E, 3) | (D, 2) | (A, 1) | (D, 2) | (C, 6) |
On valide le noeud E.
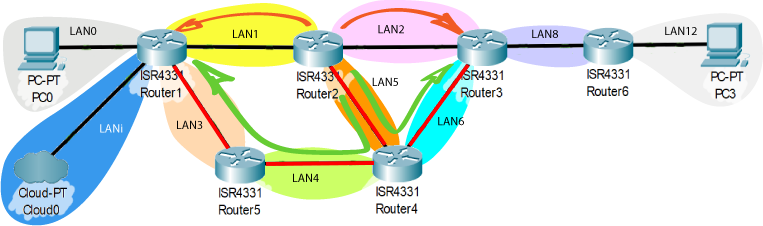
Table de routage R2 (Source) théorique
Après avoir déroulé l'algorithme, on peu déterminer les routes suivantes :
Les réseaux sont notés comme dans le premier schéma
| Type route | IP vers le LAN | IP passerelle | Interface | DA | Coût OSPF |
|---|
| C | IP LAN1 | IP R2.LAN1 | R2.LAN1 | 0 | 4* |
| C | IP LAN2 | IP R2.LAN2 | R2.LAN2 | 0 | 4* |
| C | IP LAN5 | IP R2.LAN5 | R2.LAN5 | 0 | 1* |
| O | IP LAN6 | IP R4.LAN5 | R2.LAN5 | 110 | 2 |
| O | IP LAN4 | IP R4.LAN5 | R2.LAN5 | 110 | 2 |
| O | IP LAN3 | IP R4.LAN5 | R2.LAN5 | 110 | 3 |
| O | IP LAN0 | IP R4.LAN5 | R2.LAN5 | 110 | 3 |
| O | IP LAN8 | IP R4.LAN5 | R2.LAN5 | 110 | 6 |
| O | IP LAN12 | IP R4.LAN5 | R2.LAN5 | 110 | 6 |
| O* | IP LANi | IP R4.LAN5 | R2.LAN5 | 110 | 3 |
(*) Remarquer que pour LAN1 (lan2 ou lan5), si la métrique OSPF = 4, comme le réseau est directement connecté, la distance dministrative est = 0.
Cempndant, cela ne présume pas qu'on passe à travers R1 pour rejoindre d'autres réseaux à partir de R2
Les couleurs plus sombres marquent la différence entre l'adresse de la passerelle et celle de l'interface du routeur
O* est la route par défaut candidate.
Table de routage R2 (Source) réelle
En fait, OSPF est capable de "summarizer", condenser les routes qui passent par le même lien. Il produira donc la table réelle suivante :
| Type route | IP vers le LAN | IP passerelle | Interface | DA | Coût OSPF |
|---|
| C | IP LAN1 | IP R2.LAN1 | R2.LAN1 | 0 | 4* |
| C | IP LAN2 | IP R2.LAN2 | R2.LAN2 | 0 | 4* |
| C | IP LAN5 | IP R2.LAN5 | R2.LAN5 | 0 | 1* |
| O* | 0.0.0.0/0 | IP R4.LAN5 | R2.LAN5 | 2 | |
Table de routage R4
Chaque routeur fait aussi le calcul, mais de son propre point de vue.
Ça nous donne la LSDB de R4 suivante :
| Étape | Noeuds | A | B | C | D | E | F |
|---|
| Coût depuis A |
1 | 2 |
1 | 0 |
1 | 5 |
|---|
| Init | {A, B, C, D, E, F} | (Ø, ∞) | (Ø, ∞) | (Ø, ∞) | (Ø, ∞) | (Ø, ∞) | (Ø, ∞) |
| 1 : D | {A, B, C, E, F} |
(D, 1) | (Ø, ∞) | (D, 1) | (D, 0) | (D, 1) | (Ø, ∞) |
| 2 : A | {B, C, E, F} |
(D, 1) | (A, 5) | (D, 1) | (D, 0) | (D, 1) | (Ø, ∞) |
| 3 : C | {B, E, F} |
(D, 1) | (A, 5) | (D, 1) | (D, 0) | (D, 1) | (C, 5) |
| 4 : E | {B, E, F} |
(D, 1) | (E, 2) | (D, 1) | (D, 0) | (D, 1) | (C, 5) |
| 5 : B | {B, E, F} |
(D, 1) | (E, 2) | (D, 1) | (D, 0) | (D, 1) | (C, 5) |
| 6 : F | {B, F} |
(D, 1) | (E, 2) | (D, 1) | (D, 0) | (D, 1) | (C, 5) |
Puis la table théorique de routage résultante :
| Type route | IP vers le LAN | IP passerelle | Interface | DA | Coût OSPF |
|---|
| C | IP LAN4 | IP R4.LAN4 | R4.LAN4 | 0 | 2* |
| C | IP LAN5 | IP R4.LAN5 | R4.LAN5 | 0 | 1* |
| C | IP LAN6 | IP R4.LAN6 | R4.LAN6 | 0 | 2* |
| O | IP LAN1 | IP R2.LAN5 | R4.LAN5 | 110 | 1 |
| O | IP LAN2 | IP R2.LAN5 | R4.LAN5 | 110 | 1 |
| O | IP LAN3 | IP R5.LAN4 | R4.LAN4 | 110 | 1 |
| O | IP LAN0 | IP R5.LAN4 | R4.LAN4 | 110 | 2 |
| O | IP LAN8 | IP R3.LAN6 | R4.LAN6 | 110 | 2 |
| O | IP LAN12 | IP R3.LAN6 | R4.LAN6 | 110 | 5 |
| O* | IP LANi | IP R5.LAN4 | R4.LAN4 | 110 | 2 |
(*) Remarquer que pour LAN1 (lan2 ou lan5), si la métrique OSPF = 4, comme le réseau est directement connecté, la distance dministrative est = 0.
Cependant, cela ne présume pas qu'on passe à travers R1 pour rejoindre d'autres réseaux à partir de R2
Et,enfin, la table réelle de routage résultante :
Rappel : La route choisie par le routeur pour un paquet sera la route la plus adaptée à l'adresse de destination du paquet.
L'ordre des routes n'a pas d'importance, même si on écrit (à la main) les adresses connectées en premier et la route par déafaut en dernier
| Type route | IP vers le LAN | IP passerelle | Interface | DA | Remarque |
|---|
| C | IP LAN4 | IP R4.LAN4 | R4.LAN4 | 0 | connecté |
| C | IP LAN5 | IP R4.LAN5 | R4.LAN5 | 0 | connecté |
| C | IP LAN6 | IP R4.LAN6 | R4.LAN6 | 0 | connecté |
| O | IP LAN1 | IP R2.LAN5 | R4.LAN5 | 110 | |
| O | IP LAN2 | IP R2.LAN5 | R4.LAN5 | 110 | |
| O | IP LAN8 | IP R3.LAN6 | R4.LAN6 | 110 | |
| O | IP LAN12 | IP R3.LAN6 | R4.LAN6 | 110 | |
| O* | 0.0.0.0/0 | IP R5.LAN4 | R4.LAN4 | 110 | vers LAN3, 0 et i |
Si on utilise les adresses vues au début du document, on obtient finalement :
| réseau destination | IP vers le LAN | IP passerelle | Interface | DA | Remarque |
|---|
| C | IP LAN4 : 192.168.64.0/24 | IP R4.LAN4 | R4.LAN4 | 0 | LAN4 connecté |
| C | IP LAN5 : 192.168.80.0/24 | IP R4.LAN5 | R4.LAN5 | 0 | LAN5 connecté |
| C | IP LAN6 : 192.168.96.0/24 | IP R4.LAN6 | R4.LAN6 | 0 | LAN6 connecté |
| O | IP LAN1 : 192.168.16.0/24 | IP R2.LAN5 | R4.LAN5 | 110 | |
| O | IP LAN2 : 192.168.32.0/24 | IP R2.LAN5 | R4.LAN5 | 110 | |
| O | IP LAN8 : 192.168.128.0/24 | IP R3.LAN6 | R4.LAN6 | 110 | |
| O | IP LAN12 : 192.168.192.0/24 | IP R3.LAN6 | R4.LAN6 | 110 | |
| O* | 0.0.0.0/0 | IP R5.LAN4 | R4.LAN4 | 110 | vers lans 3 (192.168.48.0/24) , 0 (192.168.0.0/24) et i (FAI) |
Et, en condensant les routes :
| Type route | IP vers le LAN | IP passerelle | Interface | DA | Remarque |
|---|
| C | 192.168.64.0/24 | 192.168.64.2 (R4.LAN4) | R4.LAN4 (192.168.64.2) | 0 | LAN4 connecté |
| C | 192.168.80.0/24 | 192.168.80.1 (R4.LAN5) | R4.LAN5 (192.168.80.1) | 0 | LAN5 connecté |
| C | 192.168.96.0/24 | 192.168.96.1 (R4.LAN6) | R4.LAN6 (192.168.96.1) | 0 | LAN6 connecté |
| O | 192.168.16.0/24 | 192.168.80.2 (R2.LAN5) | R4.LAN5 (192.168.80.1) | 110 | LAN1 |
| O | 192.168.32.0/24 | 192.168.80.2 (R2.LAN5) | R4.LAN5 (192.168.80.1) | 110 | LAN2 |
| O | 192.168.128.0/17 | 192.168.96.2 (R3.LAN6) | R4.LAN6 (192.168.96.1) | 110 | LAN 8+12 |
| O* | 0.0.0.0/0 | 192.168.64.2 (R5.LAN4) | R4.LAN4 (192.168.64.1) | 110 | vers lans 3 (192.168.48.0/24) , 0 (192.168.0.0/24) et i (FAI) |
Les routes vers LAN1 et LAN2 ne peuvent pas être condensées car l'octet à cheval sur le masque (resp. 0001 0000 et 0010 0000) pourraient être confondu avec le LAN3 qui est en 48 : (0011 0000).
Ce serait possible si on change l'adresse du lan3 en 112 (0111 0000)