Bool et binaire

L'algèbre de bool (ou booléene) est une technique de calcul logique avec des affirmations qui sont vraies ou fausse, 1 ou 0.
Les affirmations sont des conditions dont le résultat est binaire.
Exemples :

• il pleut : le résultat est vrai ou faux.
• il fait froid : le résultat est vrai ou faux.
• 5 est plus grand que 6 : le résultat est aussi vrai ou faux et pas autre chose (dans un espace euclidien ...).

Les conditions sont remplacées par des lettres comme les nombres en mathématique. Ainsi :

• il pleut sera a et
• il fait froid sera b.

Connaître l'algèbre de Bool est utile en programmation, pour déterminer les tests qui s'enchaînent

• si ciel=bleu et température=chaud ou ciel=noir et … est traduit en binaire

Mais aussi pour des variables binaires :

• capteur de ligne = 100 (4) = trop à gauche ; 010 (2) = centré ; 001(1) = trop à droite
• état : 001=enregistré, 011 = enregistré+ vu, 111 = enregistré, vu et validé

Et surtout pour le réseau et la détermination des adresse IP, Masques associés, sous-réseaux, etc...

Calculs booléens

les calculs booléens représentent les choix que l'on peut effectuer.
On dispose de trois opérations : le ET (and), le OU (or) et la négation, l'inverse : NON.
Les affirmations avec lesquelles on fait les calculs n'ont que deux possibilités : VRAI ou FAUX. VRAI est représenté par 1 et FAUX par 0.

Opérateur NON booléen

Si a = vrai, NON(a) = faux.

Opérateur ET booléen

Soit la demande suivante : j'ai vraiment envie de me promener et je suis plutôt motivé. Donc, je ne reste chez moi que s'il pleut et qu'il fait froid.
Exemple : si il pleut (a) je reste à la maison, si il ne pleut pas (NON(a)) je peux me promener. Voici les affirmations :

• a = il pleut, dans ce cas, je reste à la maison, sinon je peux me promener.
• b = il fait froid, dans ce cas, je reste à la maison et sinon je peux me promener.

 
	Il pleut ET il fait froid alors je reste chez moi => a ET b.

table de vérité :

Je ne reste à la maison que s'il pleut et qu'il fait froid.

Opérateur OU booléen

Soit la demande suivante : S'il fait beau ou s'il fait chaud, je mets un t-shirt.
Voici les affirmations :

• a = il fait beau, je mets un t-shirt, sinon je mets autre chose (un ciré, une veste, une chemise ?).
• b = il fait chaud, je mets un t-shirt et sinon je mets autre chose (un pull, une veste, un annorak ?).

table de vérité :

Je mets un t-shirt dès lors qu'il fait beau ou qu'il fait chaud.

Table de vérité complète

Voici tous les cas des opérations logiques ET et OU et leur résultat (0= faux, 1= vrai) :

• ET : si a et b = vraies, alors r = vrai ; r= faux dans tous les autres cas
• OU : si a et b = faux, alors r = faux ; r= vrai dans tous les autres cas

Équations booléennes remarquables

	a ET a = a
	a ET non(a) = faux
	a OU non(a) = vrai
 
	Commutativité de ET et OU : a ET b = b ET a ; a OU b = b OU a
	Priorité de ET sur OU : a ET b ou c = (a ET b) OU c
	Distributivité de ET sur OU : a ET (b ou c) = (a OU b) ET (a OU c)
 
	non (a ET b) = NON(a) OU NON(b)
	non (a OU b) = NON(a) ET NON(b)
 

On peut assimiler le comportement de ET et OU aux opérations décimales x et +.

Numération binaire, Pourquoi ?

Le binaire n'est pas important en soi. Mais il permet de mieux comprendre le fonctionnement des ordinateurs. Principalement il servira pour la compréhension de l'adressage IP mais aussi pour la définition des conditions dans les tests et boucles. Nous verrons ici :

• la définition des bases de numération en mathématique (le retour)
• une approche de l'algèbre de bool
• la numération binaire de base
• les conversions et leur usage en réseau
• les calculs binaires avancés

En informatique, on utilise plusieurs systèmes de base de numération :

• la base dix, le système décimal,
• la base 2, le binaire,
• la base 8, système octal et
• la base 16, hexadécimal.

Une base de numération défini le nombre de symboles différents permettant de compter jusqu'à la base.
Exemples :

• base 10 = 10 symboles, de 0 à 9,
• base 6 = 6 symboles, de 0 à 5 (les doigts de la main),
• base 2 = 2 symboles, 0 et 1 (ON/OFF, une lampe, le courant électrique est là ou non),
• base 16 = 16 symboles ???!! en base 16, on utilise les symboles de 0 à 9 et on continue avec les lettres A à F pour représenter les "chiffres" de 10 à 15,
  

A partir du moment où on dépasse le nombre maxi de symboles, il faut en ajouter un second, à gauche, pour marquer ce dépassement.
Exemples :

• En base 10 : 9+1 = 10. C'est à dire ...

	- 9+1=0 et 
	- je retiens 1 que j'ajoute au second chiffre à gauche, la dizaine. 
	- on obtient bien : unité = 9+1= **0** et dizaine = 0+la retenue de 1 = **1** soit **1 0** (prononcer *un-zéro*).
	- Noter que le maximum avec 2 chiffres est de 99. audelà, il faut un 3ème chiffre : 100  
 

• En base 6 : 5 doigts +1 doigt = 10 aussi. Impossible de représenter 6 avec une seule main. C'est à dire ...

	- 5 doigts +1 doigt = 0 doigts à la main droite et 
	- je retiens 1 que j'ajoute à la main gauche, la "*sizaine*". 
	- on obtient bien : unité = 5+1= 6 avec 1 doigt à la main gauche et 0 doigts à la main droite soit **1 0** (prononcer *un-zéro*).  
	- Maintenant, le maximum avec 2 mains est de 55. au delà, il faut emprunter une main à quelqu'un d'autre : 100
 

• En base 2 : 1+1 = 10 aussi.

	- 1+1 = 0 et je retiens 1
	- et j'ajoute la retenue au bit de gauche, la "*deuzaine*". 
	- on obtient bien : 1+1 =  **10** (prononcer *un-zéro*).
 

• En base 16 : F+1 = 10 aussi.

	- F+1 = 0 et je retiens 1
	- et j'ajoute la retenue au chiffre de gauche, la "*seizaine*". 
	- on obtient bien : F+1 =  **10** (prononcer *un-zéro*).
	- Preuve : F=15, 1=1, 10(16)=16(10).

Chaque chiffre correspond à une puissance de la base.
Ainsi, en base dix, 123 = 3x10^0 + 210^1 + 110^2 = 3 + 20 + 100 = 123. cqfd Dans les autres bases, c'est aussi le cas :

• base 2 : 101 = 12^0 + 02^1 + 12^2 = 1+0+4 = 5 en base 10.
• base 16 : 14B = B16^0 + 416^1 + 116^2 = 11+64+256 = 331 en base 10. (Rappel : A=10, B=11)

Petit quizz

• Combien de symboles a-t-on si on considère les doigts des deux mains ?
• Jusqu'à combien peut-on compter en base 2 avec 8 positions binaires ?
• Jusqu'à combien peut-on compter en base 16 avec 2 positions hexadécimales ?

Opérations de calculs

Les opérations sur des bases numériques de calcul sont comme en base 10 : addition, soustraction, multiplication et division.
Je ne présente que l'addition en plusieurs bases, pas les autres du fait de leur peu d'intérêt.

Addition

• base 10 : 6+7 = 10+3 : on compte selon 6+7 = 3 "et je retiens 1 que j'ajoute à la dizaine". Soit 6+7= 3 +110
• base 2 : 0+0=0 ; 0+1=1 ; 1+0=1. Jusque là, tout va bien mais ... 1+1=0 !!! en fait, 1+1=0 et je retiens 1 que j'ajoute à la "deuzaine" supérieure. c'est à dire 1+1 = 10 !
• base 16 : 6+7 = D (13) : on compte de 1 à F!
• base 16 : 8+8 = 10. eh oui, 8+8=16 en base 10 mais 1x16^1+0x16^0=10 en base 16.

Soustraction

Là, il vaut mieux poser le calcul :

• base 2 : 0-0=0, 1-0=1, 1-1=0 et 0-1 = - et je retiens 1 à soustraire à la deuzaine supérieure soit l'opération binaire suivante :

11 0011 (= 51)
-   101 (= 5)
_1_1__) retenue négative
10 1110 (=32+8+4+2=46 = 51-5 cqfd)

Multiplication

Très simple, c'est comme une multiplisation normale sauf qu'on a que des 1 ou des 0.
On reprend la base du calcul comme en classe de 6ème et on comprend que ce sont des multiplications par 1 ou 0 puis des additions.

Exemple : l'opération binaire 515 :

   11 0011 (= 51)
 x     101 (= 5)
 _________	=> multiplication avec décalage selon la position des chiffres
           (retenues de l'addition)
   11 0011 (= 51)
        0  (= 0 )
 1100 11   (= 51*4)
 __________ (retenues de l'addition)
 1111 1111 (= 128+64+32+16+8+4+2+1 = 255)

Division

1111 1111 | 101      "en 1, combien de fois va 1 ? ..."
          |_______   
          |
          |

Je vous laisse faire ...

Petit quizz

Calculer :

• 11011101 + 11100
• 123 + 456 en base 8 et en base 16

C'est la plus compliqué et en même temps le plus utile.
Pour faire la conversion, il existe (au moins) deux méthodes dans chaque sens. À vous de choisir celle que vous préférez.

les puissances de 2

Il est nécessaire de connaître les puissances de 2 pour effectuer les calculs (au moins de 0 à 10).
Calculatrice ou de tête ? Clairement, de tête on va plus vite. Voici les puissances de 2 qui correspondent aux rangs des chiffres en commençant par la droite (les unités).

2^16 = 65 536 = nombre de couleurs pour un pixel en 4 octets : rvb+n = qualité des images d'une imprimante classique ...

Conversion base 2 à 10

On effectue la conversion suivante : 11001010(2) -> ?(10)

Méthode 1

Commencer à droite : compter la position des 1 et additionner les puissances de 2 de ces positions (on commence à 0)

• On utilise la position en partant de la droite vers la gauche pour
• Calculer les puissances de 2 de chaque position,
• Chaque puissance est multipliée par le chiffre binaire 0 ou 1 de la position et
• On additionne le tout pour obtenir le résultat en base 10.

Méthode 2

Commencer à gauche : multiplier le résultat de n-1 et ajouter le bit n. (le + rapide ?)

• a chaque chiffre du nombre binaire,
• on ajout 0 ou 1 au résultat précédent,
• on fait une multiplication par 2.
• le total final est le nombre converti.

Sous forme algébrique : R= ((((((12+1)2+0)2+0)2+1)2+0)2+1)2+0

Méthode 3

Cette méthode est plus rapide mais ici, il faut connaître ses tables de multiplication et de conversion …

Décomposer le binaire en deux quartets :

	11001010 = 1100 0000 + 0000 1010 = 192+10 = 202

Explications :

	Q1= 1100 = 12 et Q2= 1010 = 10 ; 
	r = Q1*16+Q2 = 12*16 + 10 
	r = 160+32 + 10 = 202. 
	cqfd

Exercice

Convertir de base 2 à 10 (méthode au choix)

• 111
• 1110
• 10101010
• 11001100

Conversion base 10 à 2

Effectuer la conversion de : 166(10) => ?(2).

Méthode 1

Méthode : Soustraire des puissances de 2 par ordre décroissant.

• si le résultat est positif, on indique un 1, sinon un zéro et
• on reporte le résultat en dessous
• fin du calcul quand on a atteint le rang 2^0

Méthode 2

Méthode : effectuer des divisions entières successives jusqu'à un résultat de zéro.

• Effectuer une division entière par 2,
• Indiquer le reste et reporter le résultat en dessous
• Fin du calcul quand on a atteint un résultat de 0.

À la fin, compléter par des 0 à gauche du résultat pour avoir des octets. /ex. : 5010= 1100102 => 0011 0010

Exercice

Convertir de base 10 à 2 (méthode au choix)

• 4
• 10
• 128
• 127
• 187

Conversions en base hexadécimale

Rappels :

• base 16 : 16 symboles de 0 à 9 et A à F
• base 2 : 2 symboles => 0 et 1
• base 10 : 10 symboles => de 0 à 9

Remarque : la conversion de base 10 en 16 et inversement est plus facile si on passe par le binaire, au moins pour les lettres.
En effet, l'hexadécimal est en fait une représentation condensée du binaire, : A=1010, B= 1011, F=1111
De la même façon, il est très avantageux de présenter les nombre binaires sous forme de quartets, groupes de 4 bits.

Conversion de 2 à 16 ou 16 à 2

Conversion assez facile de 2 à 16 et 16 à 2 :

• Séparer le nombre binaire en quartets (4 bits)
• Compléter les quartets
• Convertir chaque quartet individuellement de tête ou avec l'abaque donnée en fin de ce document.

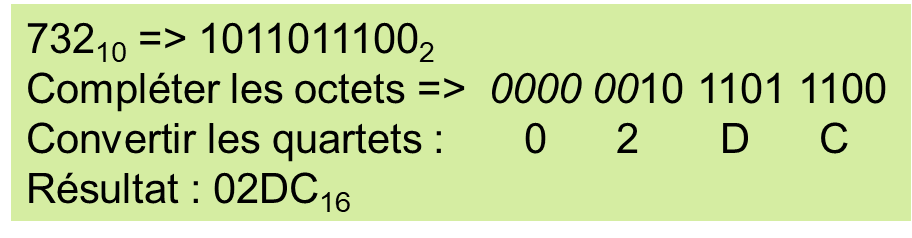
Normalement, on complète aussi les octets en plaçant autant de zéros que nécessaire devant le nombre pour obtenir un nombre de bits multiple de 8, de 16, etc...

Conversion de 10 à 16 ou 16 à 10

Un peu plus compliquée ! donc passer par le binaire :

• convertir chaque chiffre hexa en binaire : A = 1010, 5 = 0101, B = 1011
• convertir le résultat binaire en décimal : 1010 0101 1011

Une autre méthode est d'utiliser la méthode 3 de 2 à 10 mais avec des puissances de 16 ... à la calculatrice !

Les conversions représentées ci-dessous sont à apprendre par coeur.
C'est nécessaire car ils sont hyper courants dans l'adressage réseau et dans les calculs binaires.

Nombres de 0 à 15

Nombres en puissances de 2

Nombres binaires remarquables

Ces nombres sont surtout utilisés en réseau pour l'adressage IP.

Effectuer les opérations suivantes dans la base proposée et vérifier en convertissant les nombres et résultats en décimal

• Binaire :
  • 10 + 10
  • 1010 - 1
  • 1001001 + 111001
  • 1001001 OU 111001
  • 1001001 ET 111001
• Hexadécimal :
  • 10 + 10
  • 7F + 1
  • 39 + 73
  • 39 + 37